तर्कसंगत और असमर्थ संख्याओं के बीच का अंतर

शब्द "संख्याएं" हमारे दिमाग में लाती हैं जो आमतौर पर शून्य से अधिक सकारात्मक पूर्णांक मानों के रूप में वर्गीकृत किए जाते हैं। संख्याओं के अन्य वर्गों में पूर्ण संख्याएं और अंश , जटिल और असली संख्याएं और नकारात्मक पूर्णांक मानों ।

संख्याओं के वर्गीकरण को आगे बढ़ाते हुए, हम तर्कसंगत और तर्कहीन नंबरों का सामना करते हैं एक तर्कसंगत संख्या एक संख्या है जिसे एक अंश के रूप में लिखा जा सकता है दूसरे शब्दों में, तर्कसंगत संख्या को दो अंकों के अनुपात के रूप में लिखा जा सकता है।

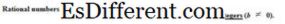
उदाहरण के लिए, संख्या 6 पर विचार करें इसे दो संख्याओं के अनुपात के रूप में लिखा जा सकता है अर्थात् 6 और 1 , अनुपात < 6/1 के लिए अग्रणी इसी तरह, 2/3 , जिसे एक अंश के रूप में लिखा गया है, एक तर्कसंगत संख्या है। इस प्रकार, हम एक तर्कसंगत संख्या को परिभाषित कर सकते हैं, एक अंश के रूप में लिखे गए संख्या के रूप में, जिसमें दोनों अंश (शीर्ष पर संख्या) और हर चीज (नीचे की संख्या) पूर्ण संख्याएं हैं परिभाषा के अनुसार, हर पूर्ण संख्या एक तर्कसंगत संख्या भी है।

दो बड़ी संख्याओं का अनुपात (

12 9, 367, 871 ) / ( 547, 724, 863 ) सरल कारण के लिए एक तर्कसंगत संख्या का एक उदाहरण भी बनाएगा, जो कि अंश और संप्रदाय दोनों पूर्ण संख्याएं हैं इसके विपरीत, कोई भी संख्या जिसे किसी अंश या अनुपात के रूप में व्यक्त नहीं किया जा सकता है उसे तर्कहीन कहा जाता है। एक तर्कहीन संख्या का सबसे अधिक उद्धृत उदाहरण

√ 2 < (< 1 414213 < …) है। एक तर्कसंगत संख्या का एक अन्य लोकप्रिय उदाहरण संख्यात्मक स्थिरांक है π ( 3.1415 9 2 … ) । -3 -> एक तर्कसंगत संख्या को दशमलव के रूप में लिखा जा सकता है, लेकिन एक अंश के रूप में नहीं। अनियमित संख्या अक्सर दैनिक जीवन में उपयोग नहीं की जाती हैं, हालांकि वे संख्या रेखा पर मौजूद हैं। संख्या रेखा पर 0 और

1

के बीच एक अनवरक्त संख्याएं अनैतिक संख्याएं हैं एक तर्कहीन संख्या में दशमलव बिंदु के दाईं ओर अंतहीन गैर दोहराए हुए अंक हैं। ध्यान दें कि निरंतर π के लिए

22/7

के बराबर उद्धृत मूल्य वास्तव में केवल एक ही है π । परिभाषा के अनुसार, एक चक्र का परिधि जो उसके त्रिज्या से विभाजित होती है वह π का ​​मान होता है यह π के कई मूल्यों की ओर जाता है, जिसमें शामिल है, लेकिन सीमित नहीं है, 333/106, 355/113 और इसी तरह 1 पर। वर्ग संख्याओं की केवल वर्ग की जड़ों; मैं। ई।, पूर्ण वर्गों की वर्ग जड़ों तर्कसंगत हैं

√ 1

= 1 (तर्कसंगत) √2

(अड़चन)

√3 (अड़ियल) √4 < = 2

(तर्कसंगत) √5, √6, √7, √8

(अड़चन) 9 9 99 = 3

(तर्कसंगत) और इतने पर। इसके अलावा, हम ध्यान दें कि, केवल n

जड़ों की n

शक्तियां तर्कसंगत हैं 64 की सारणी 64

तर्कसंगत है, क्योंकि 64 एक 6 वें शक्ति है, अर्थात् 6 < की शक्ति 2 लेकिन 6 की जड़ 63 तर्कहीन है 63 सही नहीं है 6 वें शक्ति -3 -> अनिवार्य रूप से, अपर्याप्तता का दशमलव प्रतिनिधित्व तस्वीर में आता है और कुछ रोचक परिणाम पेश करता है। जब हम एक दशमलव के रूप में तर्कसंगत संख्या को व्यक्त करते हैं, तो दशमलव में सटीक < (जैसा 1/5 = 0 होता है 20)

या यह

अयोग्य < होगा (जैसा, 1/3 ≈ 0 3333 )। या तो मामले में, अंकों का अनुमान लगाने योग्य पैटर्न होगा। ध्यान दें कि जब कोई अपर्याप्त संख्या दशमलव के रूप में व्यक्त की जाती है, तब स्पष्ट रूप से यह अचयनित होगा, क्योंकि अन्यथा, संख्या तर्कसंगत होगी इसके अलावा, अंकों की अनुमानित पद्धति नहीं होगी। उदाहरण के लिए, √2 ≈ 1 4142135623730950488016887242097 अब, तर्कसंगत संख्या के साथ, हम कभी-कभी मुठभेड़ 1/11 = 0. 0909090 । दोनों बराबर चिह्न ( = ) और तीन बिंदु ( ellipsis ) के उपयोग का मतलब है कि हालांकि

1/11

बिल्कुल भी व्यक्त करना संभव नहीं है एक दशमलव के रूप में, हम अभी भी लगभग दशमलव अंकों के साथ इसे अनुमानित कर सकते हैं जैसे कि 1/11

के करीब पहुंचने की अनुमति है इस प्रकार, 1/11

का दशमलव रूप गलत समझा जाता है एक ही टोकन से, ¼ का दशमलव रूप है जो 0. 25 है, सटीक है। तर्कसंगत संख्याओं के लिए दशमलव रूप में आना, वे हमेशा अयोग्य होने जा रहे हैं। √ 2 का उदाहरण जारी रखते हुए, जब हम √2 = 1. 41421356237 लिखते हैं … (एलिप्सस के उपयोग पर ध्यान दें), इसका तुरंत अर्थ है कि > √2

सटीक होगा इसके अलावा, अंकों की अनुमानित पद्धति नहीं होगी। संख्यात्मक तरीकों से अवधारणाओं का उपयोग करना, फिर से, हम तर्कसंगत रूप से लगभग दशमलव अंकों के लिए अनुमान लगा सकते हैं जैसे कि हम √2 के करीब हैं तर्कसंगत और तर्कसंगत संख्याओं पर कोई भी नोट अनिवार्य सबूत के बिना समाप्त नहीं हो सकता है क्यों कि √2 तर्कहीन है ऐसा करने में, हम यह भी स्पष्ट करते हैं, एक cont

आराधना द्वारा साक्ष्य का क्लासिक उदाहरण। मान लें कि √2 तर्कसंगत है यह हमें इसे दो पूर्णांक के अनुपात के रूप में दर्शाता है, कहते हैं p और q √2 = p / q कहने की ज़रूरत नहीं है, पी

और q कोई सामान्य कारक नहीं हैं, अगर कोई सामान्य कारक हो, तो हम उन्हें अंश और भाजक से बाहर।

समीकरण के दोनों किनारों को समूहीकरण, हम साथ समाप्त,

2 = p 2 / q 2

इसे आसानी से लिखा जा सकता है,

p 2 = 2q > 2 अंतिम समीकरण से पता चलता है कि पी < 2 < भी है यह तभी संभव है जब

p < स्वयं भी यहां तक ​​कि हो। इसके बदले में यह दर्शाता है कि

p

2 4 द्वारा विभाज्य है। इसलिए,

क्यू < 2 < और इसके परिणामस्वरूप

क्यू < यहां तक ​​की भी होनी चाहिए।तो p और q

दोनों भी, जो कि हमारी प्रारंभिक धारणा के विपरीत है कि उनके पास कोई सामान्य कारक नहीं हैं इस प्रकार, √2 तर्कसंगत नहीं हो सकता। प्रश्न ई। डी। <