बिजली श्रृंखला और टेलर श्रृंखला के बीच अंतर

विद्युत सीरीज बनाम टेलर श्रृंखला में एक समारोह है

गणित में, एक वास्तविक अनुक्रम वास्तविक संख्या की एक अनुक्रमित सूची है । औपचारिक रूप से, यह वास्तविक संख्याओं के सेट में वास्तविक संख्याओं के सेट से एक समारोह है। यदि एक _n एक अनुक्रम की अवधि n ^वें है, तो हम अनुक्रम को एक ₁ , द्वारा दर्शाते हैं ₂ , …, एक _n, …। उदाहरण के लिए, अनुक्रम 1, आधा, ⅓, …, ¹ / n _{, … पर विचार करें। इसे {1 / n} के रूप में चिह्नित किया जा सकता है}

अनुक्रमों का उपयोग करते हुए एक श्रृंखला को परिभाषित करना संभव है। एक श्रृंखला एक अनुक्रम की शर्तों का योग है इसलिए, प्रत्येक अनुक्रम के लिए, एक जुड़ा अनुक्रम और उपाध्यक्ष विपरीत है। यदि {a n} _{विचाराधीन अनुक्रम है, तो, उस अनुक्रम द्वारा बनाई गई श्रृंखला को इस रूप में दर्शाया जा सकता है:}

इस प्रकार, उपरोक्त उदाहरण में, संबंधित श्रृंखला 1+

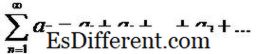
1 ^/ 2 ₊ 1 ^{/ 3} + … + ₁ / ⁿ + …। _{जैसा कि नामों का सुझाव है, बिजली श्रृंखला एक विशेष प्रकार की श्रृंखला है और यह संख्यात्मक विश्लेषण और संबंधित गणितीय मॉडलिंग में बड़े पैमाने पर प्रयोग किया जाता है। टेलर श्रृंखला एक विशेष शक्ति श्रृंखला है जो प्रसिद्ध कार्यों का प्रतिनिधित्व करने के लिए वैकल्पिक और आसान-कुशल तरीके प्रदान करती है।}

बिजली श्रृंखला क्या है?

एक शक्ति श्रृंखला फार्म की एक श्रृंखला है

जो

c

पर केंद्रित कुछ अंतराल के लिए अभिसरण (संभवतः) है। गुणांक एक n वास्तविक या जटिल संख्या हो सकती है, और एक्स से स्वतंत्र है; मैं। ई। _{डमी चर} उदाहरण के लिए, प्रत्येक n, और

c = 0, शक्ति श्रृंखला 1 + x + x के लिए _एक n = 1 सेट करके 2 + … + x n ^{+ … प्राप्त होता है यह देखना आसान है कि जब x ε (-1, 1), यह शक्ति श्रृंखला 1 / (1-x) के लिए परिवर्तित होती है।} -2 -> ^{एक शक्ति श्रृंखला जब} x

=

सी में कनवर्ज करती है। x के अन्य मूल्यों जिसके लिए शक्ति श्रृंखला परिवर्तित होती है, हमेशा सी पर केन्द्रित एक खुले अंतराल के रूप ले लेती है। यही है, एक मान 0≤ आर ≤ ∞ ऐसा होगा कि प्रत्येक x संतोषजनक | xc | ≤ R के लिए >, शक्ति श्रृंखला अभिसरण है और प्रत्येक एक्स संतोषजनक | xc |> आर के लिए, शक्ति श्रृंखला भिन्न है यह मान R को शक्ति श्रृंखला के अभिसरण के त्रिज्या कहा जाता है (आर किसी भी वास्तविक मूल्य या सकारात्मक अन्तराल ले सकता है)

पावर श्रृंखला को निम्नलिखित नियमों का उपयोग करके जोड़ा जा सकता है, घटाया, गुणा और विभाजित किया जा सकता है। दो शक्ति श्रृंखलाओं पर विचार करें: तब, -2 -> मैं। ई। जैसे शब्दों को एक साथ जोड़ा या घटाया जाता है। साथ ही, पहचान का उपयोग करके दो शक्ति श्रृंखलाओं को गुणा और विभाजित करना संभव है,

टेलर श्रृंखला क्या है?

टेलर श्रृंखला को फ़ंक्शन के लिए परिभाषित किया गया है

f

(

x

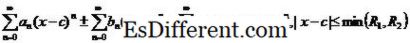
) जो एक अंतराल पर असीम रूप से भिन्न है। मान लें कि f

(

x) सी पर केन्द्रित अंतराल पर भिन्न है। तब शक्ति श्रृंखला जो <द्वारा दी गई है! --3 -> को टेलर श्रृंखला के समारोह का विस्तार f (x) के बारे में c कहा जाता है।

एक्स

= (सी) वें व्युत्पन्न x = ^ग )। संख्यात्मक विश्लेषण में, इस अनंत विस्तार में शर्तों की एक सीमित संख्या का उपयोग उन बिंदुओं पर मूल्यों की गणना में किया जाता है जहां श्रृंखला मूल समारोह के लिए अभिसरण है। एक फ़ंक्शन f ⁽ x) अंतराल (a, b) में विश्लेषणात्मक कहा जाता है, यदि प्रत्येक एक्स ε (ए, बी के लिए)), च

(x) की टेलर श्रृंखला फ़ंक्शन f (x) के लिए कनवर्ज करती है। उदाहरण के लिए, 1 / (1-x) विश्लेषणात्मक (-1, 1) है, क्योंकि इसका टेलर विस्तार 1 + x + x 2 + … + x n + … कनवर्ज ई एक्स की ई एक्स <की ^{के टेलर श्रृंखला के बाद से, उस अंतराल पर कार्य करने के लिए, और} ई ^x प्रत्येक वास्तविक संख्या के लिए x ^{पावर श्रृंखला और टेलर श्रृंखला में क्या अंतर है?} 1। टेलर श्रृंखला एक विशेष वर्ग की शक्ति श्रृंखला है जो केवल कुछ खुले अंतराल पर असीम रूप से भिन्न होने वाले कार्यों के लिए परिभाषित होती है। ^{2। टेलर श्रृंखला विशेष रूप से लेती है} जबकि, एक शक्ति श्रृंखला किसी भी श्रृंखला हो सकती है! -2 ->