चतुर्भुज और चतुर्भुज के बीच अंतर: चतुर्भुज बनाम चतुर्भुज
चतुर्भुज बनाम चतुर्भुज <बनाम है क्वाड्रिलाटरल्स और समांतरलोग्राम, यूक्लिडियन ज्यामिति में पाए जाने वाले बहुभुज हैं। समांतरलोग्राम चतुर्भुज का एक विशेष मामला है क्वाड्रिलाटरल या तो प्लेंर (2 डी) या 3 आयामी हो सकते हैं जबकि समांतरलोग्राम हमेशा प्लेंडर होते हैं।
चतुर्भुज
चतुर्भुज चार पक्षों के साथ एक बहुभुज है इसमें चार कोने हैं, और आंतरिक एंगल का योग 3600 (2π rad) है। क्वाड्रिलाटरल्स को स्व-अन्तर्विभाजक और सरल चतुर्भुज श्रेणियों में वर्गीकृत किया जाता है। स्वयं अन्तर्विभाजक चतुर्भुज में दो या दो से अधिक पक्ष एक-दूसरे को पार करते हैं, और छोटे ज्यामितीय आंकड़े (जैसे त्रिकोण चतुर्भुज के अंदर बनते हैं)।
सरल चतुर्भुज को भी उत्तल और अवतल चतुर्भुज में विभाजित किया गया है। अवतल चतुर्भुज के पास आसन्न पक्ष हैं जो आंकड़े के अंदर प्रतिबिंब के कोण को बनाते हैं। सरल चतुर्भुज के पास आंतरिक रूप से प्रतिबिंबित कोण नहीं होते हैं, उत्तल चतुर्भुज उत्तल चतुष्कोणों में हमेशा टॉसेलेलेशन हो सकते हैं
-2 ->
प्रारंभिक स्तर पर चतुर्भुज के ज्यामिति का एक प्रमुख हिस्सा उत्तल चतुर्भुजियों से संबंधित होता है कुछ क्वाड्रिलाटरल्स प्राथमिक विद्यालयों के दिनों से हमें बहुत परिचित हैं निम्न उत्तल चौगुनाहों को दिखाते हुए एक आरेख है।
-3 ->
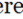
समांतरभुज को चार पक्षों के साथ ज्यामितीय आंकड़े के रूप में परिभाषित किया जा सकता है, साथ में विपरीत पक्ष एक दूसरे के समानांतर हैं। अधिक सटीक यह समानांतर पक्षों के दो जोड़े के साथ एक चतुर्भुज है। यह समानांतर प्रकृति समांतरलेग्रामों को कई ज्यामितीय विशेषताओं देती है।
एक चतुर्भुज ज्यामितीय विशेषताओं के बाद पाए जाते हैं एक समानांतर का प्रतीक है।
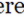

• विरोध पक्षों के दो जोड़े लंबाई में समान हैं (एबी = डीसी, एडी = बीसी)
• विरोध के दो जोड़े आकार के बराबर होते हैं। ()

• पक्षों, जो एक-दूसरे का विरोध कर रहे हैं की एक जोड़ी रहे हैं, समानांतर और लंबाई में बराबर है। (AB = डीसी और AB∥DC)
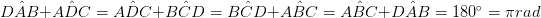
• विकर्णों एक दूसरे को द्विभाजित (ए ओ = OC, बो = ओवर ड्राफ्ट)
• प्रत्येक विकर्ण दो सर्वांगसम त्रिभुजों में चतुर्भुज बिताते हैं। (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)
इसके अलावा, पक्षों के वर्गों का योग विकर्णों के वर्गों का योग के बराबर है। इसे कभी-कभी
समांतरलोग्राम कानून के रूप में जाना जाता है और भौतिकी और इंजीनियरिंग में व्यापक अनुप्रयोग हैं (एबी 2 + बीसी 2 + सीडी 2 + डीए 2 = एसी 2 + BD 2 ) उपर्युक्त सभी गुणों को गुणों के रूप में इस्तेमाल किया जा सकता है, एक बार यह स्थापित हो गया है कि चतुर्भुज एक समानांतर चिन्ह है समांतरभुज का क्षेत्रफल एक तरफ की लंबाई के उत्पाद और ऊंचाई को विपरीत दिशा में परिकलित किया जा सकता है इसलिए, समांतरभुज का क्षेत्र
समांतरलोग्राम = आधार का क्षेत्रफल = ऊंचाई =
एबी
× एच समांतरलोग्राम का क्षेत्र अलग-अलग समानांतरचित्र के आकार से स्वतंत्र है। यह केवल आधार की लंबाई और सीधा ऊंचाई पर निर्भर है। यदि एक समानांतर रेखा के दोनों पक्षों को दो वैक्टरों द्वारा दिखाया जा सकता है, तो क्षेत्र दो आसन्न वैक्टरों के वेक्टर उत्पाद (क्रॉस उत्पाद) के परिमाण से प्राप्त किया जा सकता है यदि पक्ष एबी और ईडी क्रमशः वैक्टर (
 ) और () के द्वारा प्रतिनिधित्व किया जाता है, तो समांतरलोग्राम का क्षेत्र
) और () के द्वारा प्रतिनिधित्व किया जाता है, तो समांतरलोग्राम का क्षेत्र
द्वारा दिया जाता है, जहां α में





के लिए एक समांतरभुगतान लेता है। • एक समानांतर चार्ट में क्रम 2
की घूर्णी समरूपता है; पक्षों के समानांतर अक्षर के किसी भी आंतरिक बिंदु से दूरी का योग स्वतंत्र है बिंदु का स्थान
समांतरलोग्राम और चतुर्भुज के बीच अंतर क्या है?
• चौगुनी बहुभुज चार पक्षों के साथ (कभी-कभी टेट्रागॉन कहा जाता है) जबकि समांतरभुज एक विशेष प्रकार का चतुर्भुज है
• क्वाड्रीलाटरल्स के अलग-अलग विमानों में अपने पक्ष (3 डी स्पेस में) हो सकते हैं, जबकि समांतरलोग्राम के सभी पक्ष एक ही विमान (प्लानर / 2 आयामी) पर स्थित हैं।
• चतुर्भुज के आंतरिक कोण किसी भी मूल्य (पलटा कोणों को शामिल कर सकते हैं) जैसे कि वे 3600 तक जोड़ सकते हैं। समांतरभुगतान केवल क्यूब्स कोण के अधिकतम प्रकार के कोण के रूप में हो सकते हैं।
• चतुर्भुज के चारों ओर अलग-अलग लंबाई हो सकते हैं, जबकि समानांतर चार्ट के विपरीत पक्ष हमेशा एक दूसरे के बराबर होते हैं और लंबाई में समान होते हैं।
• कोई भी विकर्ण दो समकक्ष त्रिकोणों में समांतरलोग्राम को विभाजित करता है, जबकि एक सामान्य चतुर्भुज के विकर्ण द्वारा बनाई गई त्रिकोण आवश्यक रूप से अनुकूल नहीं होते हैं।



