व्युत्पन्न और अंतर के बीच का अंतर
व्युत्पन्न बनाम विभेदक अंतर कलन में व्युत्पन्न और एक फ़ंक्शन का अंतर निकटता से संबंधित है लेकिन बहुत अलग अर्थ हैं, और विभिन्न महत्वपूर्ण कार्यों से संबंधित दो महत्वपूर्ण गणितीय वस्तुओं का प्रतिनिधित्व करते थे
व्युत्पन्न क्या है?
किसी फ़ंक्शन के व्युत्पन्न उस दर को मापता है जिस पर फ़ंक्शन मान उसके इनपुट परिवर्तन के रूप में बदलता है बहु-चर कार्यों में, फ़ंक्शन मान में परिवर्तन स्वतंत्र चर के मूल्यों के परिवर्तन की दिशा पर निर्भर करता है। इसलिए, ऐसे मामलों में, एक विशिष्ट दिशा चुने जाते हैं और उस विशेष दिशा में कार्य को विभेदित किया जाता है। उस व्युत्पत्ति को दिशात्मक व्युत्पन्न कहा जाता है। आंशिक डेरिवेटिव एक विशिष्ट प्रकार की दिशात्मक डेरिवेटिव हैं
एक वेक्टर मूल्यवान फ़ंक्शन के व्युत्पन्नf को सीमा के रूप में परिभाषित किया जा सकता है जहां भी यह ठीक से मौजूद है जैसा कि पहले उल्लेख किया गया है, यह हमें सदिश की दिशा के साथ


हर जगह अलग-अलग है, और व्युत्पन्न सीमा के बराबर है,





f को f (1) द्वारा चिह्नित किया जाता है। अब इस नोटेशन का उपयोग करते हुए, उच्च आदेश डेरिवेटिव को परिभाषित करना संभव है। दूसरा आदेश दिशात्मक व्युत्पन्न है, और
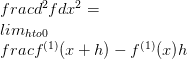

एक फ़ंक्शन का अंतर स्वतंत्र चर या चर में परिवर्तन के संबंध में फ़ंक्शन में परिवर्तन का प्रतिनिधित्व करता है। x
किसी एकल फ़ंक्शन के f किसी भी फ़ंक्शन के लिए सामान्य नोटेशन में, ऑर्डर 1 डीएफ द्वारा दिया गया कुल अंतर है, । इसका अर्थ है कि

x में एक मनमाना बिंदु x और Δ f में परिवर्तन है फ़ंक्शन में इसी परिवर्तन च । यह दिखाया जा सकता है कि Δ f = f (1) (x ) Δ x + ε, जहां ε है त्रुटि। अब, सीमा Δ x → 0 Δ f / Δ x = च (1) ( x) (व्युत्पन्न की पहले से परिभाषित परिभाषा का उपयोग करके) और इस प्रकार, Δ x → 0 ε / Δ x = 0इसलिए, यह निष्कर्ष करना संभव है कि, Δ x → 0 ε = 0. अब, denoting Δ x → 0 Δ f डी के रूप में f और Δ x → 0 Δ x जैसा कि x अंतर की परिभाषा कड़ाई से प्राप्त की जाती है उदाहरण के लिए, फ़ंक्शन के अंतर है दो या अधिक चर के कार्यों के मामले में, किसी फ़ंक्शन के कुल अंतर को प्रत्येक स्वतंत्र चर के निर्देशों में विभेदों के योग के रूप में परिभाषित किया जाता है। गणितीय, इसे के रूप में कहा जा सकता है
व्युत्पन्न और अंतर के बीच अंतर क्या है?


द्वारा दिया गया है