स्थिर और अनिश्चित एकीकृत के बीच का अंतर

< गणित की एक महत्वपूर्ण शाखा है, और भिन्नता कलन में एक महत्वपूर्ण भूमिका निभाती है। भेदभाव की उलटा प्रक्रिया को एकीकरण के रूप में जाना जाता है, और उलटा को अभिन्न, या बस रखा जाता है, भिन्नता के उलटा एक अभिन्न अंग देता है। उन निष्कर्षों के आधार पर जो निष्कर्ष उत्पन्न करते हैं, उन्हें दो वर्गों में विभाजित किया जाता है, निश्चित और अनिश्चित अनंत

निश्चित अभिन्न

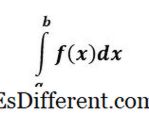
एफ (x) का एक निश्चित अभिन्न अंग है और वक्र के नीचे के क्षेत्र का प्रतिनिधित्व करता है f (x) से x = a x = b करने के लिए। एक निश्चित अभिन्न अंगों पर ऊपरी और निचली सीमाएं हैं, और इसे निश्चित कहा जाता है, क्योंकि समस्या के अंत में, हमारे पास एक संख्या है - यह एक निश्चित जवाब है।

अनिश्चित इंटीग्रल

एफ (एक्स) का अनिश्चित अभिन्न अंग एक फ़ंक्शन है और सवाल का उत्तर देता है, "विभेदित होने पर क्या कार्य देता है

f (x) ? " अनिश्चित अभिन्नता के साथ यहाँ अभिन्न पर कोई ऊपरी और निचली सीमा नहीं है, और हमें क्या मिलेगा वह जवाब है जो अभी भी

x है और इसमें एक स्थिरता भी होगी (इसमें आमतौर पर सी < द्वारा चिह्नित है

अनिश्चित अभिन्न आम तौर पर अंतर समीकरण के लिए एक सामान्य समाधान देता है।

अनिश्चित अभिन्न एकीकरण का एक सामान्य रूप है, और यह माना समारोह के विरोधी व्युत्पन्न के रूप में व्याख्या की जा सकती है।

फ़ंक्शन के भेदभाव पर विचार करें

F

किसी अन्य फ़ंक्शन की ओर जाता है f , और एफ का एकीकरण अभिन्न देता है। प्रतीकात्मक रूप से, यह एफ (x) = ∫ƒ (x) dx या

एफ = ∫ƒ डीएक्स < जहां दोनों

एफ

और

ƒ < एक्स < के कार्य हैं, और एफ अलग है उपरोक्त रूप में, इसे एक रेमैन इंटीग्रल कहा जाता है और परिणामी फ़ंक्शन एक मनमानी स्थिरांक के साथ होता है। एक अनिश्चित अभिन्न अक्सर कार्यों के परिवार उत्पन्न करता है; इसलिए, अभिन्न अनिश्चित है एकीकृत और एकीकरण प्रक्रिया अंतर समीकरण को हल करने के दिल में है हालांकि, भेदभाव के चरणों के विपरीत, एकीकरण में कदम हमेशा एक स्पष्ट और मानक दिनचर्या का पालन नहीं करते हैं। कभी-कभी, हम देखते हैं कि प्राथमिक क्रिया के संदर्भ में समाधान स्पष्ट रूप से व्यक्त नहीं किया जा सकता है। उस मामले में, विश्लेषणात्मक समाधान अक्सर एक अनिश्चित अभिन्न रूप के रूप में दिया जाता है। पथ्युलस के मौलिक प्रमेय निश्चित और अनिश्चित अभिन्न अंगों की मौलिक प्रमेय से जुड़े होते हैं: एक निश्चित अभिन्न < गणना करने के लिए, अनिश्चित अभिन्न फ़ंक्शन के एंटी-डेरिवेटिव के रूप में जाना जाता है (& quot; एंटी-डेरिवेटिव के रूप में भी जाना जाता है} और एंडपेइंट्स

x = a

और

x = b पर मूल्यांकन करें। एक ही समारोह के लिए हम एकीकरण के मूल्यांकन के बाद एक निश्चित और अनिश्चित अनंत काल के बीच का अंतर स्पष्ट होगा। निम्न इंटेग्रल पर विचार करें: ठीक है। हम दोनों को करते हैं और अंतर देखते हैं। एकीकरण के लिए, हमें सूचकांक में एक जोड़ना होगा जो हमें निम्न अभिव्यक्ति में ले जाता है: इस समय < सी < केवल हमारे लिए एक स्थिर है < सी < के सटीक मूल्य को निर्धारित करने के लिए समस्या में अतिरिक्त जानकारी की आवश्यकता है आइए हम अपने निश्चित रूप में उसी अभिन्न का मूल्यांकन करें। ई।, ऊपरी और निचले सीमाओं के साथ शामिल हैं ग्राफिक रूप से बोलते हुए, अब हम वक्र के तहत क्षेत्र की गणना कर रहे हैं

f (x) = y

3

के बीच

y = 2

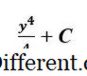
और y = 3 >। इस मूल्यांकन में पहला कदम अनिश्चित अभिन्न मूल्यांकन के समान है। फर्क सिर्फ इतना है कि इस बार हम लगातार < सी < जोड़ नहीं करते इस मामले में अभिव्यक्ति निम्नानुसार दिखती है: यह बदले की ओर जाता है:

मूलतः, हमने 3 और उसके बाद 2 को अभिव्यक्ति में बदल दिया और उन दोनों के बीच अंतर प्राप्त किया।

यह निरंतर सी < पहले के उपयोग के विपरीत निश्चित मूल्य है ^{कुछ और विस्तार से लगातार कारक (अनिश्चितकालीन अभिन्नता के संबंध में) का पता लगाएं} यदि y 3 3y

2 का अंतर है, फिर ∫

3y

2

डा 0 = 99

3 हालांकि, 3y

2

कई भाव के अंतर हो सकते हैं जिनमें से कुछ में y ³ -5 , > y ³ +7

, आदि … इसका मतलब यह है कि उत्क्रमण उलटा नहीं है क्योंकि ऑपरेशन के दौरान निरंतर बेहिसाब है। सामान्य तौर पर, ^3y 2

y 3 < + सी < जहां ^{सी < किसी भी निरंतर संयोग से, सी को} 'एकीकरण के निरंतर' के रूप में जाना जाता है ^{हम इसे इस रूप में लिखते हैं:} ∫ 3y 2 ^{dx = y} 3 + सी

एक अनिश्चित अभिन्न के लिए एकत्रीकरण तकनीकों, जैसे कि टेबल लुकअप या रीस्च एकीकरण, एकीकरण प्रक्रिया के दौरान नई विघटन को जोड़ सकते हैं। ये नई असंतोष प्रकट होते हैं क्योंकि विरोधी-डेरिवेटिव को जटिल लॉगरिदम की शुरुआत की आवश्यकता होती है। ^{तर्कसंगत नकारात्मक अक्ष को पार किया जाता है, और जब एकीकरण एल्गोरिदम कभी-कभी एक प्रतिनिधित्व प्राप्त नहीं कर पाता है, जहां इन छलांग रद्द हो जाते हैं, तो कॉम्प्लेक्स लॉगरिदम में एक छलांग असंतुलन होता है।}

यदि निश्चित अभिन्न का पहला अभिकलन एक अनिश्चित अभिन्न अभिकलन द्वारा किया जाता है और इसके परिणामस्वरूप एकीकरण की सीमाएं प्रतिस्थापित कर लेते हैं, तो हमें अवगत होना चाहिए कि अनिश्चितकालीन एकीकरण अपरदनशीलता पैदा कर सकता है। अगर ऐसा होता है, इसके अतिरिक्त, हमें एकीकरण अंतराल में असंतुलन की जांच करनी होगी।