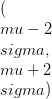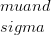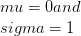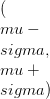द्विपद और सामान्य वितरण के बीच का अंतर

द्विपद विमा सामान्य वितरण

यादृच्छिक चर की संभाव्यता वितरण आंकड़ों के क्षेत्र में एक महत्वपूर्ण भूमिका निभाते हैं। उन प्रायिकता वितरणों में से, द्विपद वितरण और सामान्य वितरण वास्तविक जीवन में दो सबसे अधिक होने वाले हैं।

द्विपदीय वितरण क्या है?

द्विपदीय वितरण संभवतः यादृच्छिक चर एक्स, से संबंधित संभाव्यता वितरण है जो कि स्वतंत्र हां / कोई प्रयोगों के एक परिमित अनुक्रम की सफलताओं की संख्या है जिनमें से प्रत्येक की संभावना है सफलता की पी एक्स की परिभाषा से, यह स्पष्ट है कि यह एक असतत यादृच्छिक चर है; इसलिए, द्विपद वितरण असतत भी है।

वितरण को X ~ बी (n, पी) के रूप में चिह्नित किया गया है जहां n प्रयोगों की संख्या है और पी सफलता की संभावना है संभावना सिद्धांत के अनुसार, हम यह निर्धारित कर सकते हैं कि B (n, p) संभावना जन समारोह इस समीकरण से, यह अनुमान लगाया जा सकता है कि

एक्स, ई (एक्स) = एनपी और एक्स का विचरण >, वी (एक्स) = एनपी (1- पी)। उदाहरण के लिए, एक सिक्का को 3 गुना मारने का एक यादृच्छिक प्रयोग पर विचार करें। एच प्राप्त करने के रूप में सफलता को परिभाषित करें, टी प्राप्त करने में विफलता और यादृच्छिक चर एक्स प्रयोग में सफलताओं की संख्या के रूप में। तब एक्स ~

बी

(3, 0. 5) और एक्स द्वारा दिया जाने वाला संभाव्यता जन समारोह। इसलिए, कम से कम 2 एच प्राप्त करने की संभावना पी (एक्स ≥ 2) = पी (एक्स = 2 या एक्स

= 3) = पी (< एक्स = 2) + पी (एक्स = 3) = 3 सी 2 (0। 5 2) (0. 5 1 ^{) +} 3 _सी 3 ^{(0। 5} 3 ^{) (0। 5} 0) = 0. 375 + 0. 125 = 0. 5.

सामान्य वितरण क्या है? _{सामान्य वितरण संभाव्यता घनत्व समारोह,} द्वारा परिभाषित निरंतर संभावना वितरण है। पैरामीटर ^{ब्याज की आबादी का मतलब और मानक विचलन को दर्शाता है जब} वितरण मानक सामान्य वितरण कहा जाता है ^{-2 ->} यह वितरण सामान्य माना जाता है क्योंकि ज्यादातर प्राकृतिक घटनाएं सामान्य वितरण का पालन करती हैं। उदाहरण के लिए, मानव आबादी के बुद्धि आम तौर पर वितरित किया जाता है। जैसे कि ग्राफ़ से देखा गया है कि यह बगैर, मतलब और घंटी के आकार के बारे में सममित है। मतलब, मोड, और औसत दर्जे का है। वक्र के क्षेत्र में आबादी के हिस्से से मेल खाती है, दी गई स्थिति को संतोषजनक है।

अंतराल में आबादी का अंश

, ,

लगभग 68 है2%, 95. 6% और 99. 8% क्रमशः।

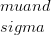
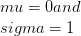
द्विपद और सामान्य डिस्ट्रीब्यूशन में क्या अंतर है?

द्विपदीय वितरण एक पृथक संभावना वितरण है जबकि सामान्य वितरण एक निरंतर है

द्विपदीय वितरण की संभाव्यता का सामूहिक कार्य है, जबकि सामान्य वितरण की संभावना घनत्व का कार्य है

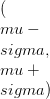
द्विपदीय वितरण कुछ शर्तों के तहत सामान्य वितरण के साथ अनुमानित है, लेकिन अन्य तरीकों से नहीं।