केंद्रवर्ती सर्कसेंटर इनसेंटर और ऑथोसेनेटर के बीच अंतर। Centroid vs Circumcenter vs Incenter vs Orthocenter

सर्कसेंटर, इनसेंटर, ऑथोस्कोनेटर बनाम Centroid

सर्कसेंटर: circumcenter तीन त्रिकोण के सीधा द्विभाजक के चौराहे का बिंदु है परिमांसर केंद्र का परिधि है, जो एक त्रिकोण के तीनों कोने से गुजरने वाला एक चक्र है

circumcenter को आकर्षित करने के लिए त्रिभुज के दोनों तरफ कोई दो लंबवत द्विभाजक बनाएँ। चौराहे के बिंदु से circumcenter देता है कम्पास और शासक के सीधे किनारे का उपयोग करके एक द्विभाजक बनाया जा सकता है। कम्पास को त्रिज्या में सेट करें, जो लाइन सेगमेंट की आधी की तुलना में अधिक है फिर से चाप के केंद्र के रूप में अंत के साथ खंड के दोनों तरफ दो चाप बनाएँ। इस खंड के दूसरे छोर के साथ प्रक्रिया को दोहराएं। चार आर्क्स सेगमेंट के दोनों तरफ दो बिंदु के चौराहे बनाते हैं। शासक की सहायता से इन दो बिंदुओं में शामिल होने वाली रेखा खींचना, और यह खंड के लंबवत द्विभाजक को दे देगा।

परिवृत्त को बनाने के लिए, circumcenter के साथ एक चक्र को केंद्र के रूप में खींचें और circumcenter के बीच की लंबाई और सर्कल के त्रिज्या के रूप में एक शीर्ष।

इनसेंटर:

इनसेंटर तीन कोण बिष्ठा एस के चौराहे का बिंदु है। इनसेंटर सर्कल का केंद्र परिधि त्रिकोण के सभी तीनों तरफ छेदते हुए है। -3 -> एक त्रिकोण के इनसेंटर को आकर्षित करने के लिए, किसी भी दो आंतरिक त्रिभुज के कोण बिस्टिकर्स बनाएँ दो कोण द्विभाजक के चौराहे के बिंदु इनसेंटर को देता है। कोण द्विभाजक को आकर्षित करने के लिए, एक ही त्रिज्या के साथ प्रत्येक हथियारों पर दो आर्क्स बनाएं। यह कोण के बाहों पर दो बिंदु (प्रत्येक हाथ पर एक) प्रदान करता है फिर केंद्र के रूप में हथियारों पर प्रत्येक बिंदु लेते हुए, दो और चाप आकर्षित करें इन दो आर्कों के चौराहे द्वारा निर्मित बिंदु तीसरे बिंदु देता है। कोण के शीर्ष में शामिल होने वाली रेखा और तीसरे बिंदु कोण द्विभाजक देता है

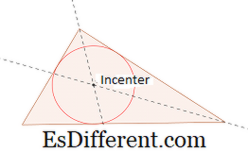
अन्तराल बनाने के लिए, किसी भी ओर लंब रेखा खंड बनाना, जो इनसेंटर से गुजर रहा है। त्रिज्या के रूप में लंबवत और इनसेंटर के बीच की लंबाई लेना, एक पूर्ण चक्र बनाएं। ऑर्थोसेनेटर: ऑर्थोसेनेटर त्रिभुज की तीन ऊंचाई (ऊंचाई) के चौराहे का बिंदु है ऑर्थोसेनेटर बनाने के लिए, किसी दो

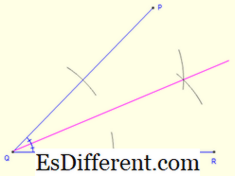
त्रिकोण के ऊँचाई निकालें विपरीत दिशा से गुजरने वाली तरफ एक रेखा खंड को एक ऊंचाई कहा जाता है।किसी बिंदु से गुजरने वाली एक लंब रेखा खींचना, केंद्र के रूप में बिंदु के साथ लाइन पर पहले दो आर्चें चिह्नित करें। इसके बाद, केंद्र के रूप में प्रत्येक चौराहे के साथ एक और दो आर्क्स बनाएं पहले बिंदु और अंतिम निर्माण बिंदु में शामिल होने वाले रेखा सेगमेंट को आकर्षित करें, और यह लाइन खंड को लंबवत रेखा देता है और पहले बिंदु से गुजरती है। दो ऊंचाइयों के चौराहे के बिंदु ओर्थसेंटर को देता है Centroid:

Centroid तीन एक त्रिभुज के मध्यियों

के चौराहे का बिंदु है Centroid प्रत्येक मध्यक 1: 2 अनुपात में विभाजित करता है, और एक समान, त्रिभुज लैमीना के द्रव्यमान का केंद्र इस बिंदु पर स्थित है। केन्द्रक का निर्धारण करने के लिए त्रिकोण का कोई दो मध्यस्थ बनाएं। मध्य बनाने के लिए, एक तरफ के मध्य बिंदु को चिह्नित करें फिर मध्य रेखा से जुड़ने वाले रेखा सेगमेंट का निर्माण करें और त्रिभुज के विरोध के शीर्ष पर। मध्यस्थों के चौराहे के बिंदु एक त्रिभुज का केंद्र देता है सर्कसेंटर, इनसेंटर, ऑथोसेनेटर और सँट्रॉइड में अंतर क्या है?

• परिमार्जन त्रिभुज के लंबवत द्विभाजकों का उपयोग करके बनाया गया है। • त्रिकोण के कोण बिग्मेककों का उपयोग करके इनसेंटर बनाया गया है • ऑर्थोसेनेटर त्रिकोण के ऊंचाइयों (ऊंचाई) का उपयोग करके बनाया गया है • त्रिकोणीय के मध्यकों का उपयोग करके Centroid बनाया गया है

• दोनों circumcenter और incenter विशिष्ट ज्यामितीय गुणों के साथ हलकों जुड़ा हुआ है

• केंद्रवर्ती

त्रिभुज के ज्यामितीय केंद्र है, और यह एक समान त्रिकोणीय लामिना के द्रव्यमान का केंद्र है

• गैर समभुज त्रिकोण के लिए, circumcenter, orthocenter, और केंद्र एक सीधी रेखा पर स्थित है, और लाइन को

यूलर लाइन

के रूप में जाना जाता है